Manual

The calculation of the fractal dimension of macromolecules from their atomic structure is a new feature available from the July 2024 US-SOMO release. It was implemented during an investigation into the reason behind the relatively small differences in computing the hydrodynamic parameters between the GRPY and ZENO methods (see the "History" section in the main US-SOMO Help), but it could find other applications, and for this reason it is offered to the general user.

The first section of this panel present the general Fractal Dimension options:

• First, the choice between the three different methods that are available (one of which with two options), as can be seen from the pull-down menu under Method:

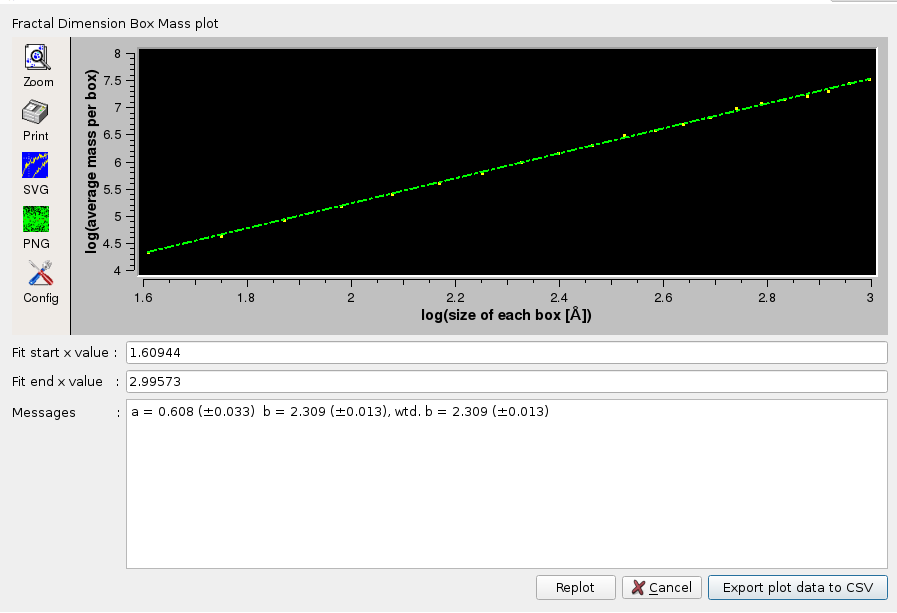
  The first method is a general box counting algorithm that returns the mass fractal dimension D_m, as decribed in Liebovitch and Toth, "A fast algorithm to determine fractal dimensions by box counting.", Phys. Lett. A, 141:386-390, 1989. To compute the fractal dimension via Box Mass, the program iterates Number of Steps times from Start [Å] to End [Å]. For each step, a grid of boxes is placed over the protein. The average mass of each box containing at least one atom of the protein is computed. The logarithm of the average mass per box versus the logarithm of the edge size of each box is collected (and optionally plotted). The slope of this line, determined through linear regression, provides an estimate of the fractal dimension.

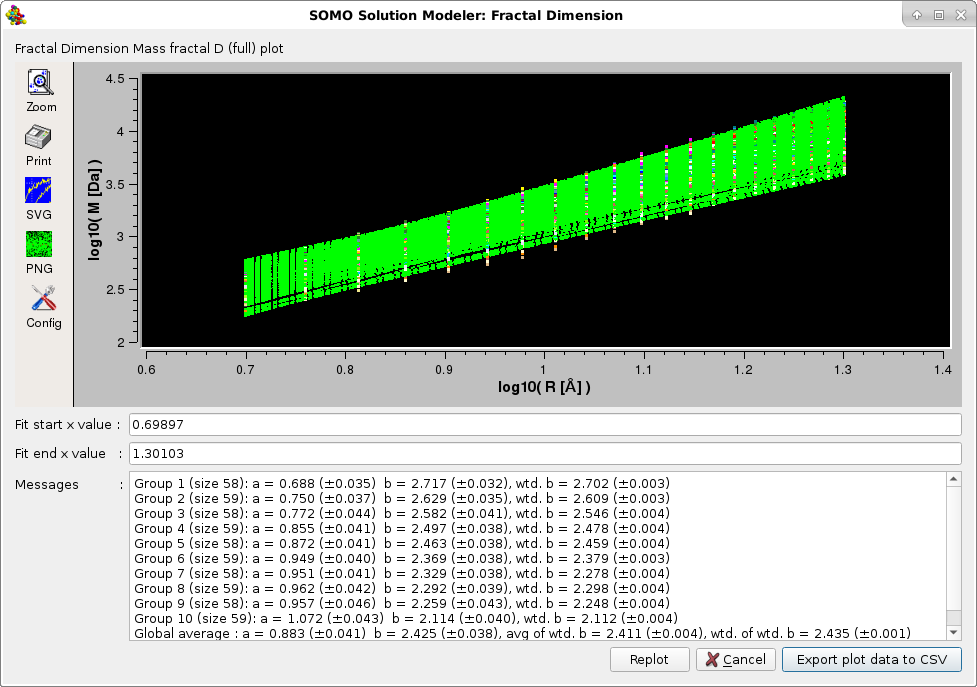
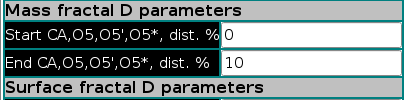
  The second and third options also provide the mass fractal dimension D_m, following the work of Enright and Leitner, ("Mass fractal dimension and the compactness of proteins", Phys. Rev. E 71, 011912-1/9, 2005), where the structure is divided in "slices" selecting the nearest CA atoms within 10%, 10-20 %, 20-30 %, etc. from the center of mass of the protein. Each set is used as centers of concentric spheres or radius R containing atoms of total mass M, and D_m is computed as the slope of the plot of log₁₀ M vs log₁₀ R. D_m can be evaluated from a particular "slice" (Mass Fractal D (slice) option), or as an average between all slices (Mass Fractal D (full) option). See the Enright and Leitner paper for a full description of this method. In our implementation, each linear fit of of log₁₀ M vs log₁₀ R produces data with SD of the intercept and slope, and D_m is calculated as the unweigthed and weighted averages (± their SD) within each slice. For the full version, an unweighted and a weighted average are calculated from the the weighted averages (± their SD). Weighting reduces the influence of poor linear regression fittings in the final results.

  The third method returns the surface fractal dimension D_s using the dependence of the accessible surface area of the structure as a function of the probe radius r, using the same rolling sphere algorithm ASAB1 as described here. Since ASA ~ r^{2 - D_s}, the slope of a double log₁₀ plot of ASA vs. r will enable the determination of D_s. See T.G Dewey, Fractals in molecular biophysics, Chapter 2 "Fractal Aspects of Protein Structure". Oxford University Press, Oxford, New York, 1997; and references therein.

  Only in Expert mode, the R_g/D_m or R_g/D_s ratios are also reported for the chosen calculations.

• The second entry, Enabled, is a checkbox for enabling the Fractal dimension calculation upon loading a structure from the main US-SOMO panel. Default: disabled.

• If the third entry Show plots checkbox is selected, the linear regressions for the selected method are automatically shown at the end of the calculations, as in the three examples below for human serum albumin (1AO6.pdb, monomer after adding missing atoms/residues):

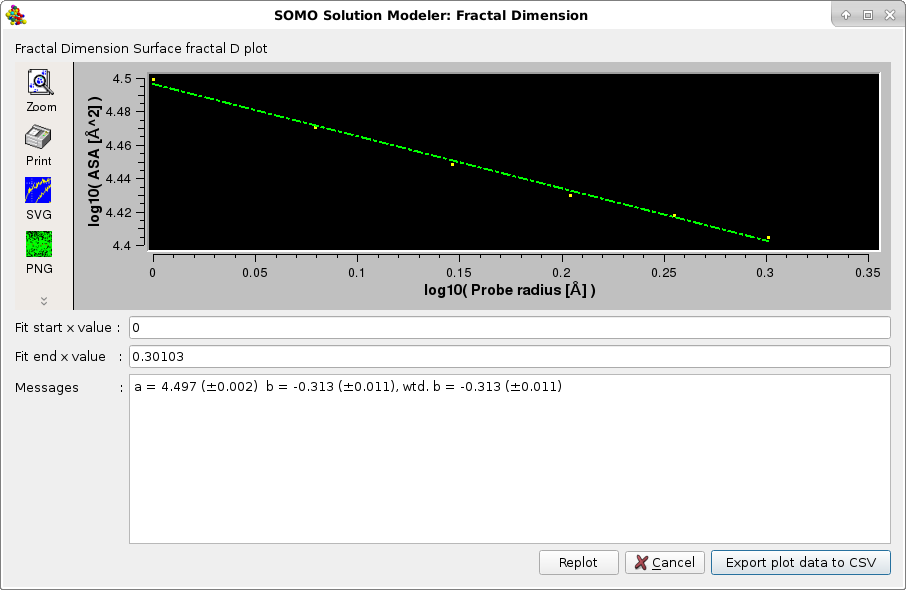  The plots are interactive, the x-axis starting and ending values can be changed and the fitting redone by pressing the Replot button. The final plots data can be saved in a csv-style file. The Default setting for this option is disabled.

• The final entry in the first section, Save plot data as csv, allows if checked the automatic saving of the regression data in a csv-style file. The Default setting for this option is disabled.

• The Start [Å] and End [Å] entries govern the range of values for computation of the Box Mass and Mass Fractal D methods, with default 5 and 10 Å, respectively. The default values seem to provide a good linear range for regression for proteins we have examined. It is recommended to verify the plots for a good linear range.

• The Number of steps from the Start [Å] to the End [Å] for computation of the Box Mass and Mass Fractal D methods, (default: 20). Increasing the Number of steps will give the linear regression more data points to fit at the cost of increase the time it takes to compute. The default value seems to be a good balance, increasing the points may provide increased accuracy.

• The Start CA, O5, O5',O5*, dist % and End CA, O5, O5',O5*, dist % set the starting and ending distances percent from the center of mass of the structure for the Mass fractal D (slice) method (also applied to the full version). The CA, O5, O5',O5* define the centers of the concentric spheres for proteins (CA) and for carbohydrates and nucleic acids (O5, O5',O5*), where we have chosen the common O5 position in the sugar ring, and " O5' " " O5* " are alternative names for this atom as found in the PDB. Defaults: 0% and 10%, respectively.

• The Probe radius start [Å], Probe radius end [Å], and Probe radius steps govern the starting and ending radii of the probe rolling sphere used in the ASAB1 routine, and the number of steps taken in going from the start to the end value. Defaults are 1 Å, 2 [Å], and 5 steps, respectively.

This document is part of the UltraScan Software Documentation distribution.
Copyright © notice.

The latest version of this document can always be found at:

http://somo.aucsolutions.com

Last modified on June 13, 2024